二叉查找树的 js 实现

2018年4月3日 · 阅读需 11 分钟

二叉树（Binary tree）是每个节点最多只有两个分支(不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”和“右子树”。二叉树的分支具有左右次序，不能颠倒。

二叉树分很多种，而二叉查找树是其中比较经典的一款，也称二叉搜索树、有序二叉树、排序二叉树，是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

节点

每个二叉树的节点有它本身的值，同时都具有左子树和右子树，根据这个定义，我们得到：

/**
 * 单个节点
 */
class Node {
  constructor(val) {
    this.val = val;
    this.left = this.right = null;
  }
}

树的结构

每一颗二叉树都必须有一个根节点 root。

/**
 * 二叉查找树
 */
class Tree {
  constructor(val = null) {
    this.root = null;
    if (val) {
      this.root = new Node(val);
    }
  }
}

添加一些方法

跟之前的链表一样，二叉查找树也会包含一些操作方法，比如 insert、remove...。

insert（插入节点）

根据二叉查找树的定义很容易推导出，将待插入的值从根节点的开始比较：

这里需要注意的一点是对root节点的判断，如果不存在，直接构建root节点。

class Tree {
  // ...
  static _insert(val, node) {
    if (val < node.val) {
      if (node.left) {
        this._insert(val, node.left);
      } else {
        node.left = new Node(val);
      }
    } else {
      if (node.right) {
        this._insert(val, node.right);
      } else {
        node.right = new Node(val);
      }
    }
  }

  insert(val) {
    if (!this.root) {
      this.root = new Node(val);
      return;
    }

    this.constructor._insert(val, this.root)
  }
  // ...
}

remove（移除节点）

这里比较复杂一点，根据二叉查找树的定义，节点间的相互关系总是以下规则，即：左子树的任意节点值 < 该节点的值 < 右子树的任意节点值，所以在移除某节点时，需要考虑右子树是否存在。如果右子树存在，将左子树移至右子树的最小节点下，然后用右子树替换被移除节点；若不存在直接用左子树替换被移除节点。

下面我用一张动画做出更好的说明：

移除节点原理

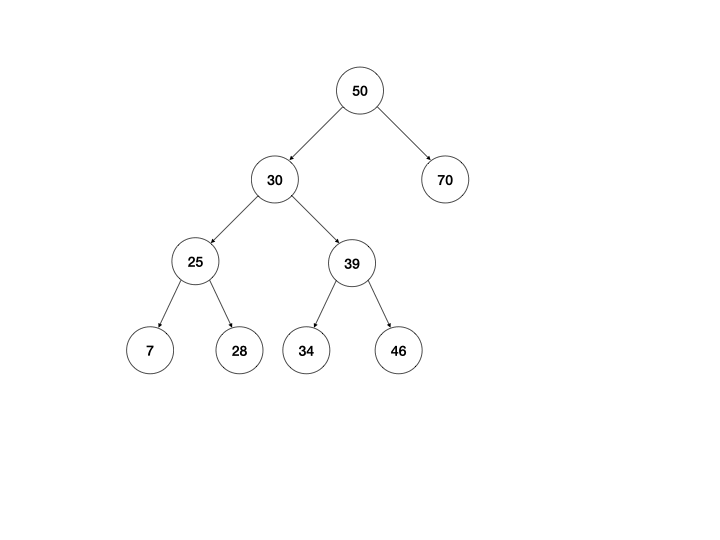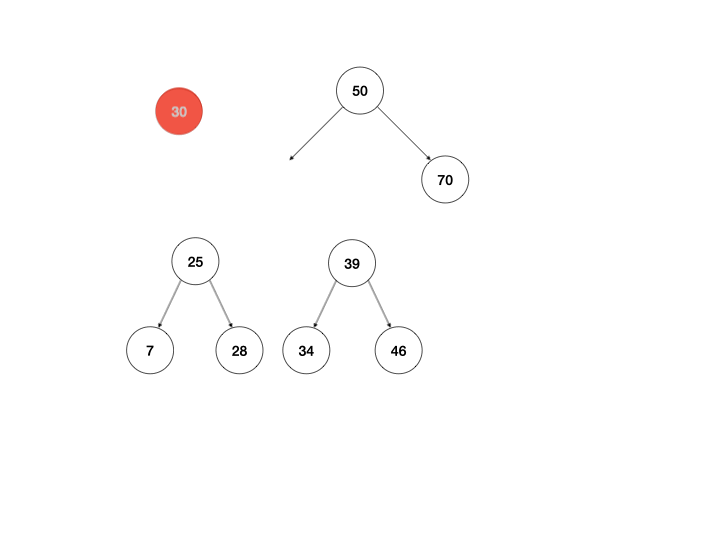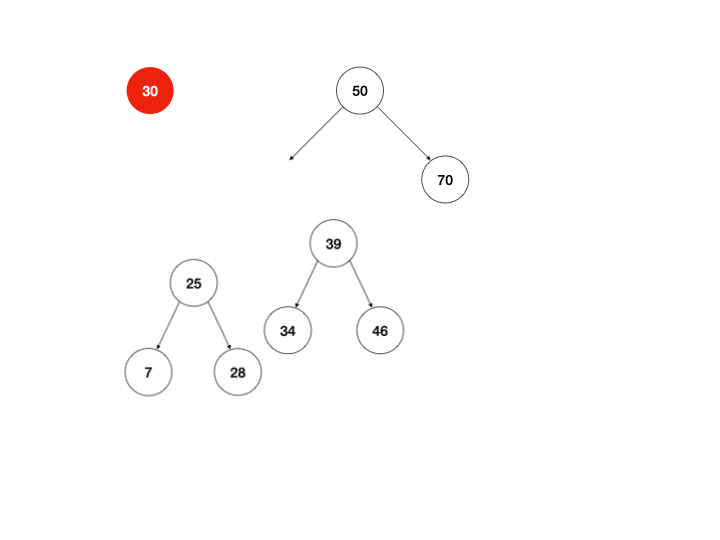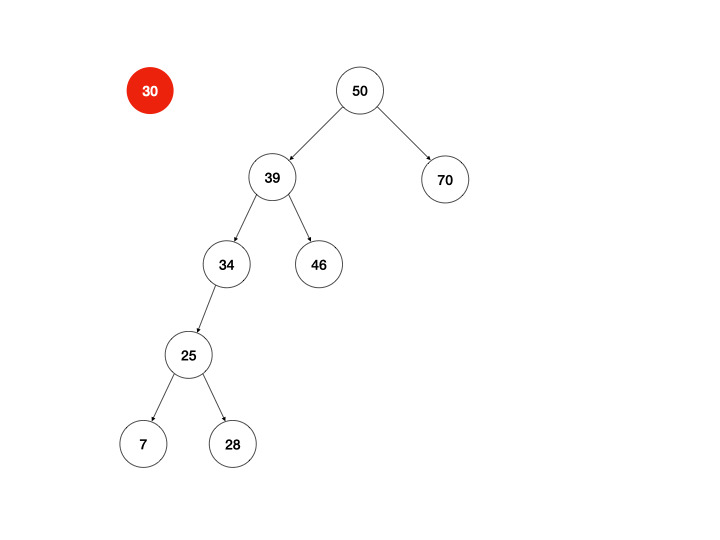
看完原理那就着手开干吧。

class Tree {
  // ...
  // 挂载的辅助函数
  static _mountMinTree(tree, host) {
    if (host.left) {
      this._mountMinTree(tree, host.left)
    } else {
      host.left = tree
    }
    return host
  }

  static _remove(val, node) {
    if (!node) {
      return null;
    }

    if (val === node.val) { // 要删除的节点是当前节点
      if (!node.right) { // 右子树不存在，直接用左子树替换当前节点流程结束
        return node.left;
      } else if (!node.left) { // 左子树不存在，直接用右子树替换当前节点流程结束
        return node.right;
      } else { // 右子树存在
        return this._mountMinTree(node.left, node.right); // 取出左子树挂载到右子树的最小节点上，返回该右子树替换当前节点
      }
    } else if (val < node.val) { // 要删除的节点在左子树
      node.left = this._remove(val, node.left);
      return node;
    } else { // 要删除的节点在右子树
      node.right = this._remove(val, node.right);
      return node;
    }
  }

  // 移除节点
  remove(val) {
    this.root = this.constructor._remove(val, this.root);
  }
  // ...
}

以上是我最开始的思路，下面还有两种方式，是我一开始未曾想到的，由于二叉查找的树定义可知，右子树的最小节点总是大于左子树的最大节点，所以可以提取左子树的最大节点/右子树的最小节点直接替换当前节点即可。

同样用动画说明：

以右子树的最小节点值替换当前节点值以左子树的最大节点值替换当前节点值

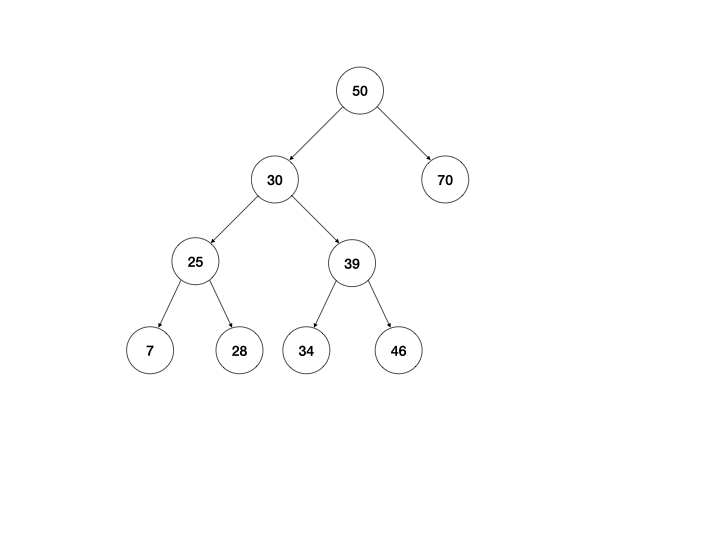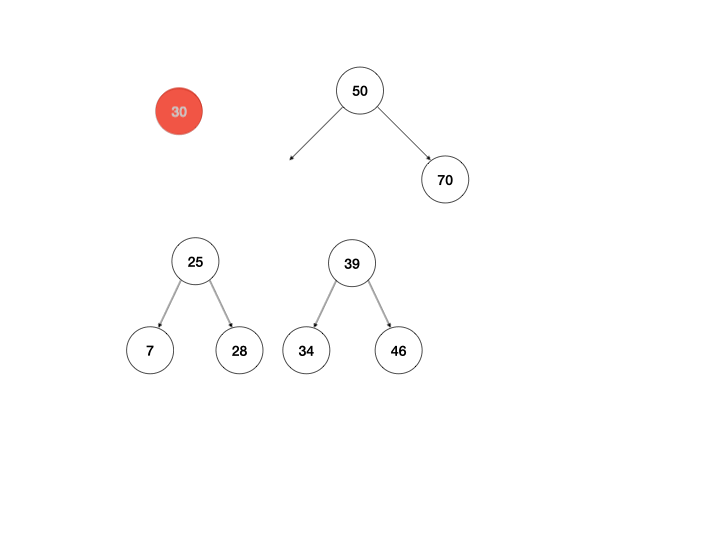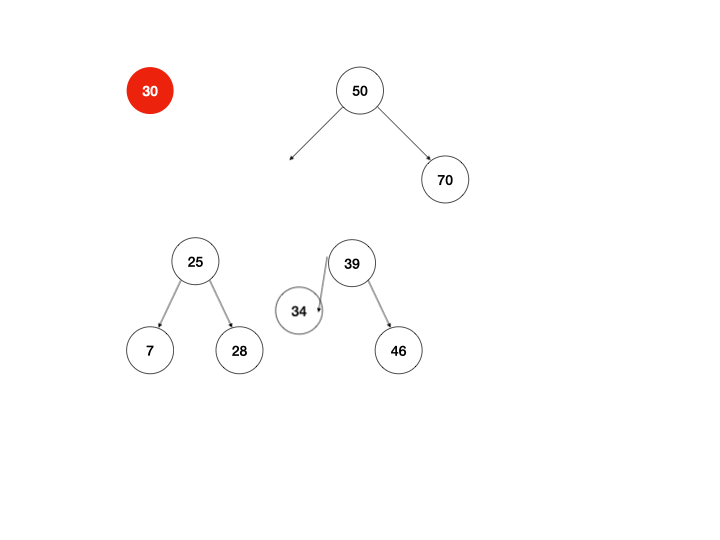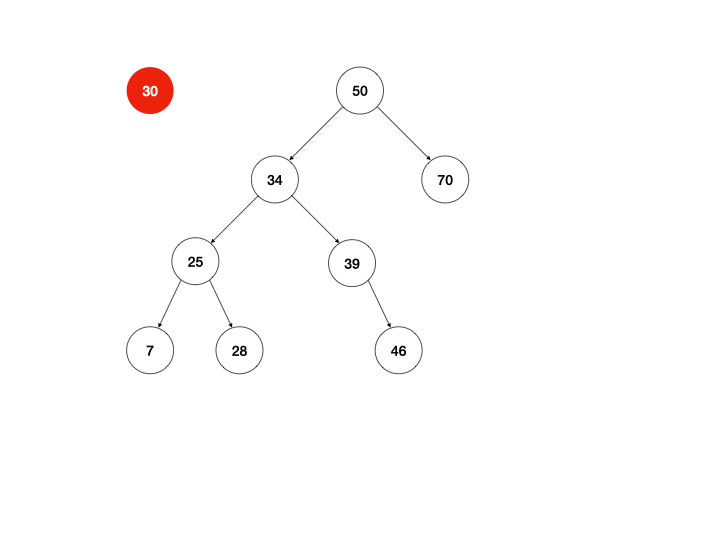
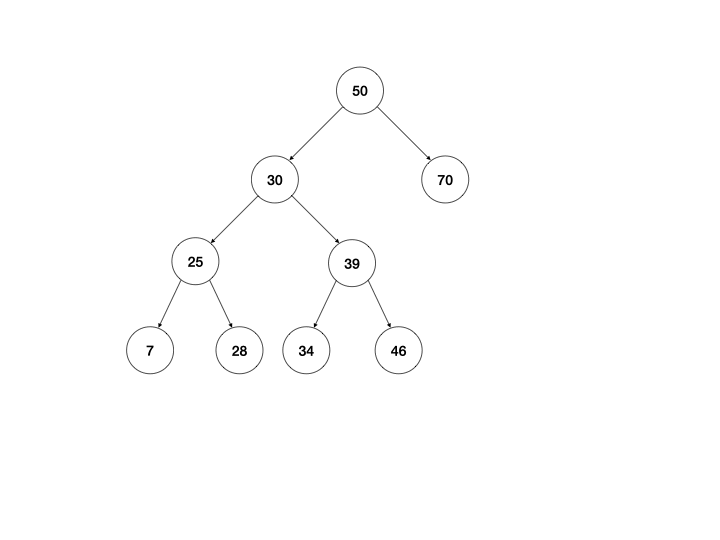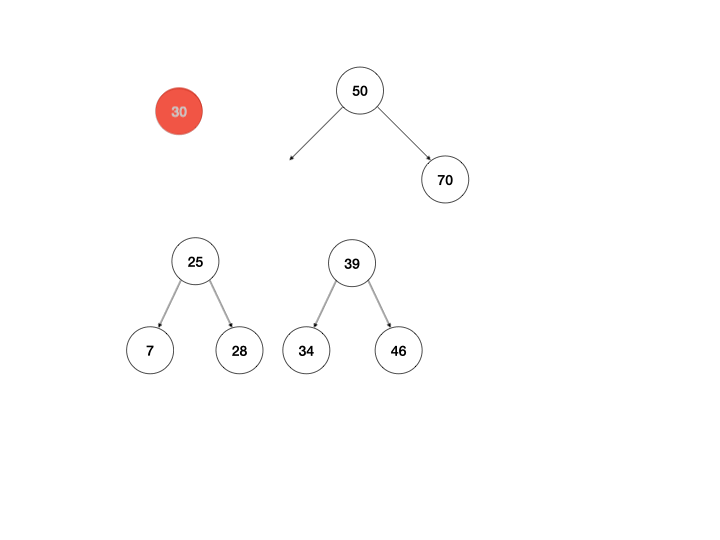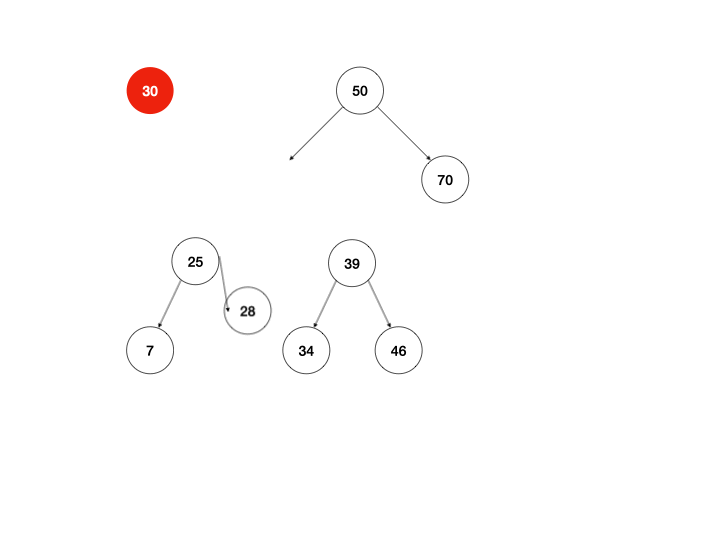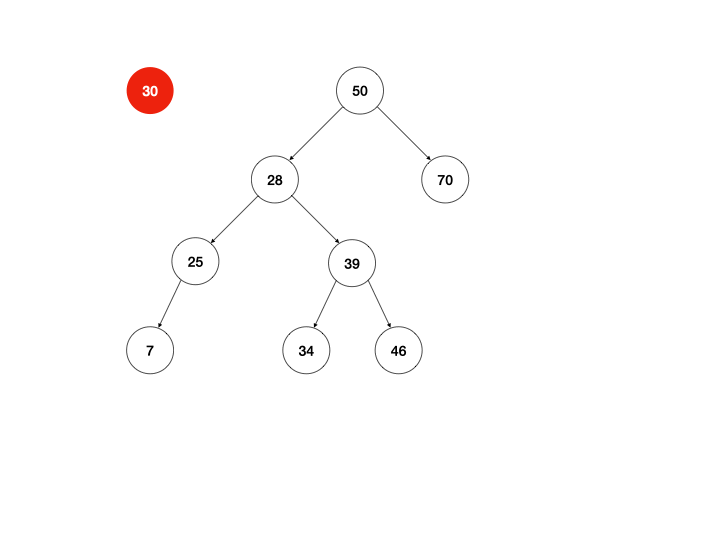
体现在算法上，区别只有return this._mountMinTree(node.left, node.right);这一行需要改写，以左图为例：

class Tree {
  // ...
  static _minNode(node) {
    if (!node) {
      return null;
    }
    while (node && node.left) {
      node = node.left;
    }
    return node;
  }

  static _remove(val, node) {
    // ...
      } else { // 右子树存在
        // return this._mountMinTree(node.left, node.right); // 取出左子树挂载到右子树的最小节点上，返回该右子树替换当前节点
        const minNode = this._minNode(node.right); // 找到右子树最小节点
        node.val = minNode.val; // 替换
        node.right = this._remove(minNode.val, node.right); // 右子树删除最小节点
        return node;
      }
    // ...
  }

  // 移除节点
  remove(val) {
    this.root = this.constructor._remove(val, this.root);
  }
  // ...
}

min/max（获取最小/最大值）

这个很简单，最小/最大值只需要循环查找左子树/右子树即可，参考上面的_minNode方法。

includes（包含）

跟数组的includes含义一样，判断是否存在指定值。

class Tree {
  // ...
  static _includes(val, node) {
    if (!node) {
      return false;
    }
    if (val === node.val) {
      return true;
    }
    return this._includes(val, val < node.val ? node.left : node.right);
  }

  includes(val) {
    return this.constructor._includes(val, this.root);
  }
  // ...
}

getMaxDepth（获取最大深度）

class Tree {
  // ...
  static _depth(node) {
    if (!node) {
      return 0
    }
    return Math.max(this._depth(node.left), this._depth(node.right)) + 1;
  }

  getMaxDepth() {
    return this.constructor._depth(this.root);
  }
  // ...
}

遍历

遍历的方式有很多中，首先分广度优先遍历（breadth-first search，BFS）和深度优先遍历（depth-first search，DFS），深度优先遍历又分前序、中序、后序，下面逐一分析。

广度优先遍历

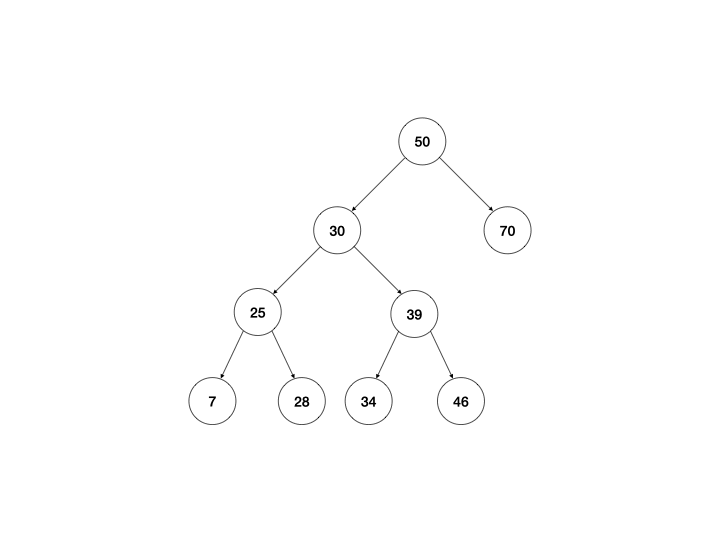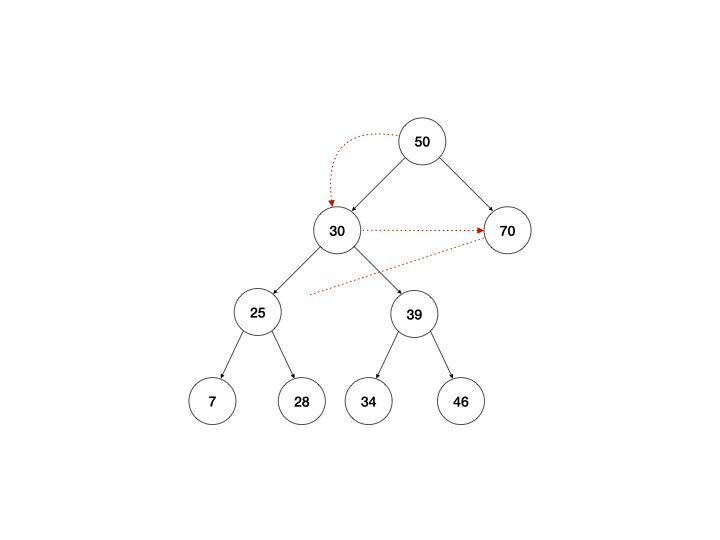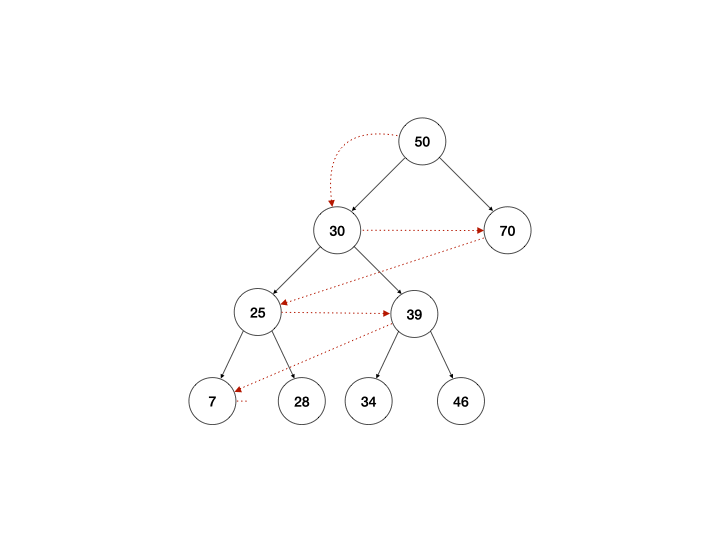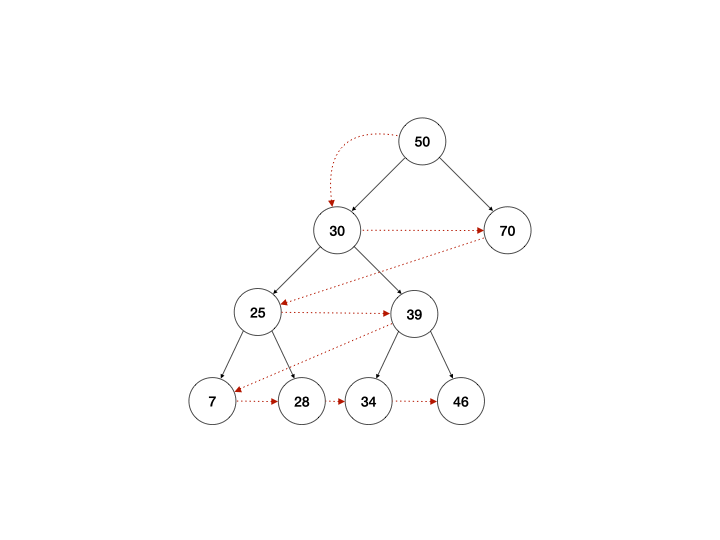
广度优先遍历的做事方式形容起来有点像画同心圆，先访问圆心点，然后标记离圆心紧邻的点，一层一层往外扩展，使用队列来操作是比较方便的：

从顶点开始，将顶点加入队列；
取出队列中的第一个节点，标记已访问；
找到第一个节点的子节点，将其加入队列；
将第一个节点从队列中移除，再次重复步骤2，直到队列中为空结束。

class Tree {
  // ...
  bfs() {
    if (!this.root) {
      return [];
    }
    const queue = [this.root];
    const list = [];
    while (queue.length) {
      const node = queue.shift();
      list.push(node.val);
      if (node.left) {
        queue.push(node.left);
      }
      if (node.right) {
        queue.push(node.right);
      }
    }
    return list;
  }
  // ...
}

深度优先遍历

深度优先遍历的做事方式形容起来就是“一条道走到黑”，对于每一个节点，在它有子节点的情况下，总是会深挖子节点，直到没有子节点后沿着原路回退到节点本身；根据节点、左子树、右子树间的访问顺序不同又细分出前序、中序、后序方法。

前序遍历：节点 -> 左子树 -> 右子树；

class Tree {
  // ...
  dfsPre(node = this.root, list = []) {
    if (node) {
      list.push(node.val);
      this.dfsPre(node.left, list);
      this.dfsPre(node.right, list);
    }
    return list;
  }
  // ...
}

中序遍历：左子树 -> 节点 -> 右子树；

class Tree {
  // ...
  dfsIn(node = this.root, list = []) {
    if (node) {
      this.dfsIn(node.left, list);
      list.push(node.val);
      this.dfsIn(node.right, list);
    }
    return list;
  }
  // ...
}

后序遍历：左子树 -> 右子树 -> 节点；

class Tree {
  // ...
  dfsPost(node = this.root, list = []) {
    if (node) {
      this.dfsPost(node.left, list);
      this.dfsPost(node.right, list);
      list.push(node.val);
    }
    return list;
  }
  // ...
}

后记

对于树的操作，我对移除操作有些疑惑，包括后来也查询了一些资料，清一色都是后面两种方案，让我一度产生对自己想到的第一种方法的正确性产生过怀疑，不过总结下来理论上应该是没错的，变换后的结果也是符合二叉查找树的定义的，只要算法上不出错就不会问题......吧？

节点​

树的结构​

添加一些方法​

insert（插入节点）​

remove（移除节点）​

min/max（获取最小/最大值）​

includes（包含）​

getMaxDepth（获取最大深度）​

遍历​

广度优先遍历​

深度优先遍历​

后记​

节点